3阶以内的矩阵求逆矩阵的3种手算方法
3阶以内的矩阵求逆矩阵的3种手算方法
求矩阵的逆具有非常重要的意义,分享一个如何针对3阶以内的方阵,求出逆矩阵的3种手算方法:待定系数法、伴随矩阵法、初等变换法
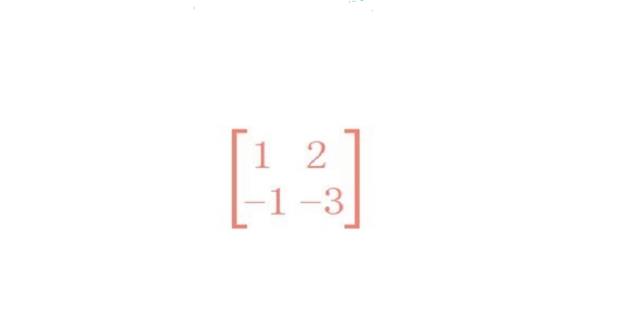
待定系数法求逆矩阵
首先,可以看如何使用待定系数法,求矩阵的逆。
举例:
矩阵A=
1 2
-1 -3
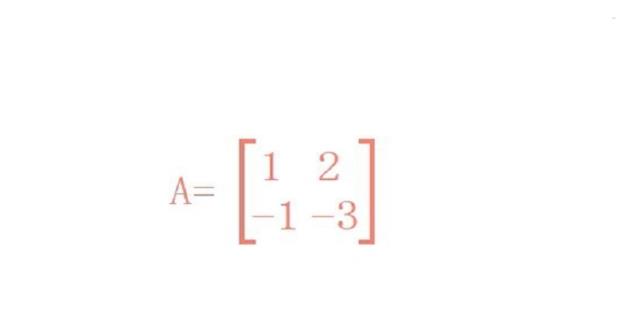
假设所求的逆矩阵为
a b
c d
则
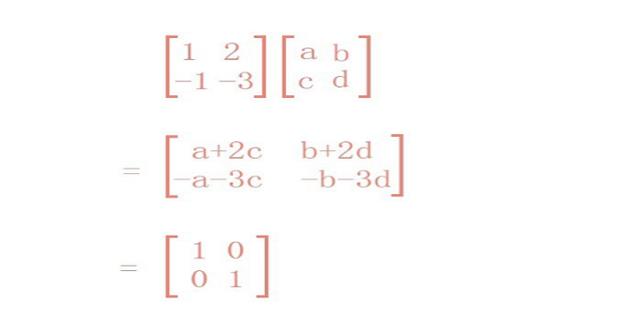
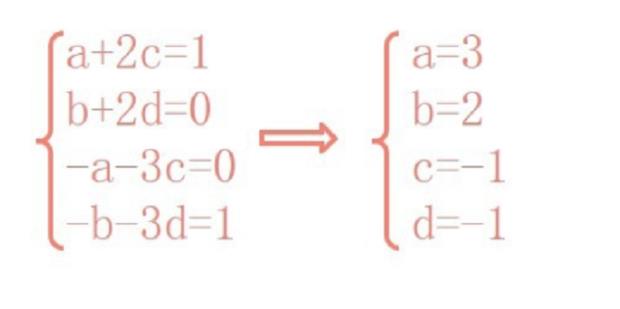
从而可以得出方程组
a+2c=1
b+2d=0
-a-3c=0
-b-3d=1
解得
a=3
b=2
c=-1
d=-1
伴随矩阵求逆矩阵
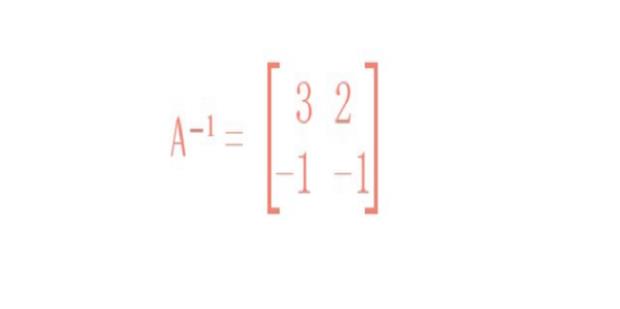
伴随矩阵是矩阵元素所对应的代数余子式,所构成的矩阵,转置后得到的新矩阵。
先求出伴随矩阵A*=
-3 -2
1 1
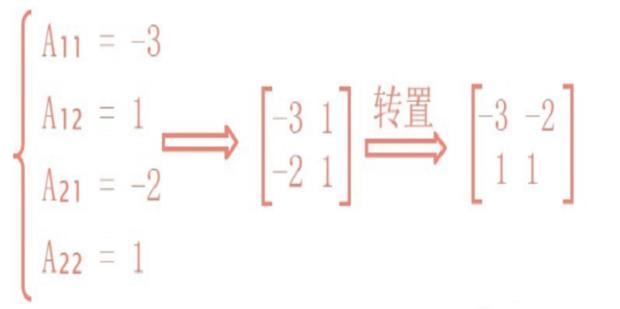
接下来,求出矩阵A的行列式
|A|
=1*(-3)-(-1)*2
=-3+2
=-1
从而逆矩阵A⁻¹=A*/|A| = A*/(-1)=-A*=
3 2
-1 -1
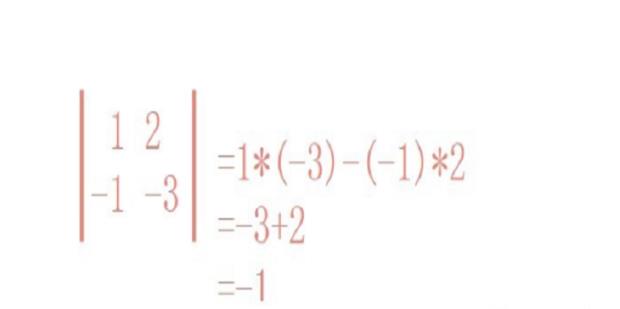
初等变换求逆矩阵
下面介绍如何通过初等(行)变换来求逆矩阵。
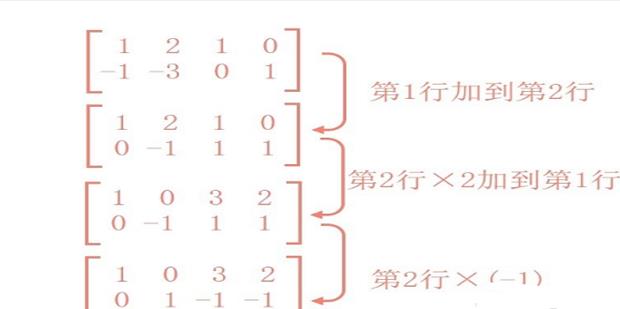
首先,写出增广矩阵A|E,即矩阵A右侧放置一个同阶的单位矩阵,得到一个新矩阵。
1 2 1 0
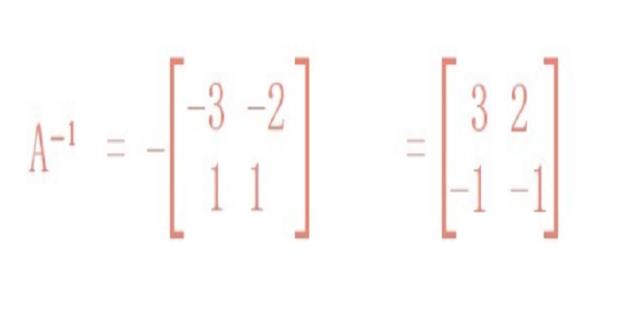
然后进行初等行变换。依次进行
第1行加到第2行,得到
1 2 1 0
0 -1 1 1
第2行×2加到第1行,得到
1 0 3 2
0 -1 1 1
第2行×(-1),得到
1 0 3 2
0 1 -1 -1

因此逆矩阵A⁻¹=
3 2
-1 -1
-

- 我的世界电脑版1.9怎么用命令方块做神弓
-
2024-04-16 21:47:52
-
- 王者荣耀-鲁班出装及铭文最强攻略
-
2024-04-16 21:45:47
-

- 如何彻底删除快压广告
-
2024-04-16 21:43:43
-
- 皮蛋自制作方法及配方
-
2024-04-16 12:32:48
-

- 酷家乐如何设计复式楼
-
2024-04-16 12:30:42
-
- 电子表格的加减乘除法
-
2024-04-16 12:28:36
-

- 企业财务管理五大重要性
-
2024-04-16 12:26:30
-

- 惠州巽寮湾双月湾旅游攻略(2天1日游)优惠攻略
-
2024-04-16 12:24:24
-

- Foobar2000如何设置最佳音质
-
2024-04-16 12:22:18
-
- lol吸血鬼怎么连招
-
2024-04-16 12:20:12
-
- 怎么利用软件录制视频教程
-
2024-04-16 12:18:06
-
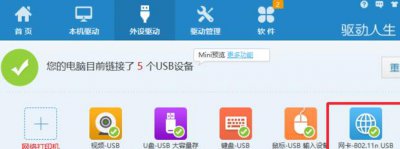
- 电脑不能识别无线网卡怎么办
-
2024-04-16 12:16:00
-

- 单位结算卡的作用
-
2024-04-16 12:13:54
-

- 钢琴五线谱学习教程
-
2024-04-16 09:08:07
-

- 电动汽车充电桩安装流程
-
2024-04-16 09:06:02
-

- 王者荣耀最新版本妲己最强出装,连坦克都不敢追
-
2024-04-16 09:03:57
-
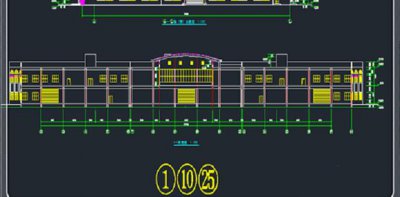
- CAD中如何输入带圈的数字
-
2024-04-16 09:01:52
-

- ISO14000认证中文证书含义介绍
-
2024-04-16 08:59:47
-

- 短跑跑步的技巧和姿势
-
2024-04-16 08:57:43
-

- 睡眠不好如何调理 12妙招让你睡个好觉
-
2024-04-16 08:55:38


 农村40万存款算穷吗
农村40万存款算穷吗 ins什么意思,女生ins是什么意思?
ins什么意思,女生ins是什么意思?