​角加速度公式与半径的关系(角加速度公式推导)

角加速度公式与半径的关系(角加速度公式推导)

角加速度公式与半径的关系，建立了一种简单有效的 *** 。通过计算得到了加速度的大小，并与实验结果进行了比较。最后，给出了一个实例，验证了本文 *** 的正确性。。该 *** 不仅适用于大型复杂结构，而且适用于非线性系统。文中所提出的算法具有良好的收敛性，可用于复杂结构的优化设计。本文的研究成果可为大型复杂结构的优化设计提供参考。同时，也为非线性系统的优化设计提供了一种新的思路。

例9一木板放在两个半径r=0.25m的传输鼓轮上面。在图示瞬时，木板具有不变的加速度a=0.5m/s2，方向向右。同时，鼓轮边缘上的点具有一大小为3m/s2的全加速度。如果木板在鼓轮上无滑动，则此木板的速度为()。

A．0.86m/s

B．3m/s

C．0.5m/s

D．1.67m/s

解：木板做平动，鼓轮做定轴转动。鼓轮边缘上的点和木板接触，故ar=a= 0.5（m/s2）

答案：A

（2010年真题）直角钢杆OAB在图所示瞬时角速度

，角加速度

若OA=40cm，AB=30cm，则B点的速度大小、法向加速度的大小和切向加速度的大小为()。

A. 100cm/s, 200cm/s2, 250cm/s2

B. 80cm/s, 160cm/s2, 200cm/s2

C. 60cm/s, 120cm/s2, 150cm/s2

D. 100cm/s, 200cm/s2, 200cm/s2

解：B点到转轴O的距离R=OB=50cm，故v=Rω=50x2=100(cm/s2)

答案：A

(2009年、2016年真题)杆OA绕固定轴O转动，长为l，某瞬时杆端A点的加速度α如图所示，则该瞬时OA的角速度及角加速度为( )。

真题2017—52题杆 OA 绕固定轴 O 转动，长为 l 。某瞬时杆端 A 点的加速度 a 如图所示，则该瞬间 OA的角速度及角加速度为（ ） 。

答案：C

(2009年真题)绳子的一端绕在滑轮上，另一端与置于水平面上的物块B相连(见图)，若物块B的运动方程为x=kt2，其中k为常数，轮子半径为R。则轮缘上A点的加速度大小为()。

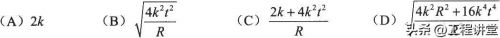
三、点的合成运动

当一点M相对于某一参考系运动，而此参考系本身又相对于惯性参考系做非惯性运动

时，点M的运动便可由两种运动组合而成，称为点的合成运动或点的复合运动。

1，动点、定系与动系的基本概念

动点：即研究对象。可能是单独的点，也可能是刚体上的某一点。

定系：工程上一般指固结于地球表面的坐标系，或固结于相对地球静止的物体上的参

考系。

动系：相对定系有运动的参考系。一般固结在与地面有相对运动的物体上。该物体称作“载体”或参考体。载体是有形的，其尺寸是有限的，而“动系”则是无形的，可以无限大，其运动属刚体运动范畴。

三者的关系：动点相对动系和定系都有运动，动系相对于定系也有运动，它们分别属于或固结于三个不同的物体。

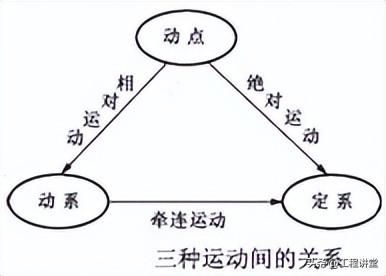
2．三种运动及其关系

(1)三种运动的定义、观察对象（研究对象）、观察点（参考体）和运动性质见表。

(2)三种运动间的关系见图。

3．速度及加速度合成定理

速度及加速度合成定理(见表)。

（2008年真题）杆OA=l，绕定轴O以角速度ω转动，同时通过A端推动滑块B沿轴x运动（见图）。设分析运动的时间内杆与滑块并不脱离，则滑块的速度VB的大小用杆的转角φ与角速度ω表示为()。

解：这是运动学中点的合成运动的内容。选OA杆上的A点为动点，选动坐标系固结在滑块B上，选定坐标系固结在地面上。

由于OA杆作定轴转动，滑块B作平动，所以动点A的绝对运动速度va、相对