​3的3次方是多少(1.03的3次方是多少)

3的3次方是多少(1.03的3次方是多少)

1、3的3次方是多少

3的3次方是多少，这个问题其实很简单，只需要将3连乘3次即可得出答案。具体计算过程如下：

3 * 3 * 3 = 27

所以，3的3次方是27。

3的3次方在数学上被称为3的立方，可以表示为3^3。在代数中，幂运算是一种重要的运算法则之一。它表示一个数连乘自己多次。

对于3的3次方，也可以理解为将3乘以它自身3次。这样的计算过程虽然简单，但是准确而严谨。通过计算，我们得出答案27。

在实际生活中，3的3次方也具有特殊的意义。例如，一个正方体的每条边的长度为3，那么它就有3条边，将体积为3 * 3 * 3 = 27。这就是3的3次方的几何意义。

除了3的3次方，我们还可以计算其他数的幂。不同的数的幂运算结果各不相同，有些可能是整数，有些可能是小数或者分数。幂运算在数学和物理等领域中有着广泛的应用，具有重要的作用。

综上所述，3的3次方是27。幂运算是一种重要的运算法则，具有广泛的应用价值。通过对幂运算的学习和理解，我们可以更好地应用它，解决实际问题。

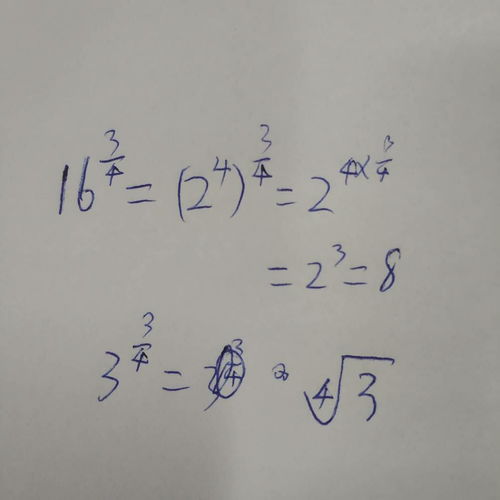
2、1.03的3次方是多少

1.03的3次方是多少

我们知道，数学是一门无穷魅力的学科，它包含了许多奇妙的数学运算和规律。其中一个常见的数学运算就是求幂。当我们要求一个数的N次方时，我们将该数自乘N次。那么，我们来探索一下1.03的3次方是多少。

要计算1.03的3次方，我们只需将1.03自乘3次。将1.03与自己相乘，我们得到1.0609。接着，将得到的结果1.0609再次与1.03相乘，我们得到1.092727。将1.092727与1.03相乘，我们得到最终结果1.12684781。

所以，1.03的3次方等于1.12684781。

那么，为什么我们要关注这个小小的数学计算呢？实际上，在实际生活中，这个计算可以有很多应用。

它可以用于计算复利。当我们存款时，银行会根据利率计算我们的利息。如果我们每年的利率为3%，那么我们的存款金额将以1.03的3次方的倍数增加。这个计算对我们了解利息的增长和积累非常有帮助。

它可以用于计算增长率。许多经济和财务领域的分析都需要计算增长率。通过求幂运算，我们可以计算某一指标在特定时间内的增长幅度。这个计算可以帮助我们了解经济和企业的发展状况。

除此之外，求幂运算还在其他科学领域中有着广泛的应用，如物理、化学等。在这些科学领域中，我们需要计算不同物理量的指数关系，这就需要用到求幂运算。

综上所述，1.03的3次方等于1.12684781。尽管这个计算看起来很简单，但它在实际生活和科学领域中有着重要的应用价值。希望通过这篇文章，大家对求幂运算的应用有了更深层次的理解。

3、3的3次方是多少怎么算

3的3次方，即3的立方，是指将3自乘3再乘3的运算结果。为了求得3的3次方，我们可以使用简单的数学方法。

我们将3自乘一次得到3，再将这个结果与3相乘，即3乘以3等于9。将得到的结果9再乘以3，即9乘以3等于27。所以，3的3次方等于27。

除了上述的逐步计算外，我们还可以使用指数运算法则来计算3的3次方。根据指数运算法则，如果a的n次方，即a^n，则表示将a自乘n次。因此，3的3次方可以写作3^3。

接下来，我们可以利用幂运算的定义，将3的3次方计算出来。根据定义，3的3次方等于3乘以3乘以3，也等于27。

在数学中，幂运算是非常重要的概念之一，它在实际问题中有着广泛的应用。无论是计算科学、物理学还是工程学，幂运算都扮演着重要的角色。

3的3次方等于27。通过逐步计算或利用指数运算法则，我们可以轻松求得3的3次方的结果。数学中的幂运算为我们解决了诸多实际问题，也带来了无限的乐趣。

4、负负3的3次方是多少

负负3的3次方是多少？这个问题看似简单，但实际上需要我们仔细思考和运用数学原理来解答。

我们需要明确一点，负数的指数运算涉及到复数和虚数的概念。在实数范围内，我们无法得到一个负数的实数次方。然而，当我们将复数和虚数引入到运算中，就能解决这个问题。

具体来说，-3可以写成-3+0i的形式，其中i是虚数单位。那么，(-3+0i)的3次方可以通过展开和运算得到。根据复数的乘法法则，我们可以将其展开为：(-3+0i)^3=(-3+0i)(-3+0i)(-3+0i)。

在计算中，我们可以采用分配律来简化运算。(-3+0i)(-3+0i)=9-0i-0i+0i^2=9-0i-0i-1，再将其与(-3+0i)相乘得到：(-3+0i)(9-0i-0i-1)=(-27+0i-0i+3)=-24+0i。

现在我们还需要将结果与(-3+0i)再次相乘，即(-24+0i)(-3+0i)。利用分配律，我们可以得到：(-24+0i)(-3+0i)=72-0i+0i+0i^2=72-0i+0i-1=71-0i。

综合以上计算，我们得出结论：负负3的3次方等于71-0i。因为实部为71，虚部为0，所以结果是一个实数。

通过对于复数乘法运算的理解和运用，我们得出了负负3的3次方的结果。这个问题提醒了我们在数学运算中的复杂性和魅力，同时也展示了数学的广阔和深邃。数学的世界是如此丰富多样，我们需要不断学习和探索，才能更好地理解和运用它。